Bài viết trình bày lý thuyết và hướng dẫn giải các dạng toán phép vị tự trong chương trình Hình học 11 chương 1. Kiến thức và các ví dụ trong bài viết được tham khảo từ các tài liệu phép dời hình và phép đồng dạng trong mặt phẳng xuất bản trên TOANMATH.com.
A. KIẾN THỨC CẦN NẮM
1. Định nghĩa phép vị tự
• Cho điểm \(I\) và một số thực \(k\ne 0\), phép biến hình biến mỗi điểm \(M\) thành điểm \(M’\) sao cho \(\overrightarrow{IM’}=k.\overrightarrow{IM}\) được gọi là phép vị tự tâm \(I\), tỉ số \(k\), ký hiệu \({{V}_{\left( I;k \right)}}.\)
• \({V_{\left( {I;k} \right)}}\left( M \right) = M’\) \( \Leftrightarrow \overrightarrow {IM’} = k.\overrightarrow {IM} .\)
2. Biểu thức tọa độ của phép vị tự
Trong mặt phẳng tọa độ \(Oxy\), cho \(I\left( {{x_0};{y_0}} \right)\), \(M\left( {x;y} \right)\), gọi \(M’\left( {x’;y’} \right) = {V_{\left( {I;k} \right)}}\left( M \right)\) thì \(\left\{ \begin{array}{l}
x’ = kx + \left( {1 – k} \right){x_0}\\
y’ = ky + \left( {1 – k} \right){y_0}
\end{array} \right.\)
3. Tính chất của phép vị tự
• Nếu \({V_{\left( {I;k} \right)}}\left( M \right) = M’\), \({V_{\left( {I;k} \right)}}\left( N \right) = N’\) thì \(\overrightarrow {M’N’} = k\overrightarrow {MN} \) và \(M’N’ = \left| k \right|MN.\)
• Phép vị tự tỉ số \(k:\)
+ Biến ba điểm thẳng hàng thành ba điểm và bảo toàn thứ tự giữa ba điểm đó.
+ Biến một đường thẳng thành đường thẳng thành một đường thẳng song song hoặc trùng với đường thẳng đã cho, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.
+ Biến một tam giác thành tam giác đồng dạng với tam giác đã cho, biến góc thành góc bằng góc đã cho.
+ Biến đường tròn có bán kính \(R\) thành đường tròn có bán kính \(\left| k \right|R.\)
4. Tâm vị tự của hai đường tròn
• Với hai đường tròn bất kì luôn có một phép vị tự biến đường tròn này thành đường tròn kia, tâm của phép vị tự này được gọi là tâm vị tự của hai đường tròn.
• Cho hai đường tròn \(\left( {I;R} \right)\) và \(\left( {I’;R’} \right).\)
+ Nếu \(I\equiv I’\) thì các phép vị tự \({{V}_{\left( I;\pm \frac{R’}{R} \right)}}\)biến \(\left( I;R \right)\) thành\(\left( I’;R’ \right)\).
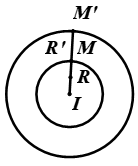
+ Nếu \(I\ne I’\) và \(R\ne R’\) thì các phép vị tự \({{V}_{\left( O;\frac{R’}{R} \right)}}\) và \({{V}_{\left( {{O}_{1}};-\frac{R’}{R} \right)}}\) biến \(\left( I;R \right)\) thành\(\left( I’;R’ \right)\). Ta gọi \(O\) là tâm vị tự ngoài còn \({{O}_{1}}\) là tâm vị tự trong của hai đường tròn.

+ Nếu \(I\ne I’\) và \(R=R’\) thì có \({{V}_{\left( {{O}_{1}};-1 \right)}}\) biến \(\left( I;R \right)\) thành\(\left( I’;R’ \right)\).

B. CÁC DẠNG TOÁN PHÉP VỊ TỰ
Dạng toán 1. Xác định ảnh của một hình qua phép vị tự
Phương pháp: Dùng định nghĩa, tính chất và biểu thức tọa độ của phép vị tự.
Ví dụ 1. Trong mặt phẳng \(Oxy\), cho đường thẳng \(d\) có phương trình \(5x+2y-7=0\). Hãy viết phương trình của đường thẳng \(d’\) là ảnh của \(d\) qua phép vị tự tâm \(O\) tỉ số \(k=-2\).
Cách 1:
Lấy \(M\left( {x;y} \right) \in d\) \( \Rightarrow 5x + 2y – 7 = 0\) \(\left( * \right).\)
Gọi \(M’\left( {x’;y’} \right) = {V_{\left( {O; – 2} \right)}}\left( M \right).\)
Theo biểu thức tọa độ của phép vị tự, ta có:
\(\left\{ \begin{array}{l}
x’ = – 2x + \left[ {1 – \left( { – 2} \right)} \right].0\\
y’ = – 2y + \left[ {1 – \left( { – 2} \right)} \right].0
\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}
x = – \frac{1}{2}x’\\
y = – \frac{1}{2}y’
\end{array} \right.\)
Thay vào \(\left( * \right)\) ta được \( – \frac{5}{2}x’ – y’ – 7 = 0\) \( \Leftrightarrow 5x’ + 2y’ + 14 = 0.\)
Vậy \(d’:5x + 2y + 14 = 0.\)
Cách 2:
Do \(d’\) song song hoặc trùng với \(d\) nên phương trình \(d’\) có dạng: \(5x + 2y + c = 0.\)
Lấy \(M\left( {1;1} \right)\) thuộc \(d.\)
Gọi \(M’\left( {x’;y’} \right) = {V_{\left( {O; – 2} \right)}}\left( M \right)\), ta có: \(\overrightarrow {OM’} = – 2\overrightarrow {OM} \) \( \Rightarrow \left\{ \begin{array}{l}
x’ = – 2\\
y’ = – 2
\end{array} \right.\)
Thay vào \(\left( * \right)\) ta được \(c = 14.\)
Vậy \(d’:5x + 2y + 14 = 0.\)
Ví dụ 2. Trong mặt phẳng \(Oxy\), cho đường tròn \(\left( C \right):{{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=4\). Tìm ảnh của đường tròn \(\left( C \right)\) qua phép vị tự tâm \(I\left( -1;2 \right)\) tỉ số \(k=3\)
Đường tròn \(\left( C \right)\) có tâm \(J\left( {1;1} \right)\), bán kính \(R = 2.\)
Gọi \(J’\left( {x’;y’} \right) = {V_{\left( {I;3} \right)}}\left( J \right)\) \( \Rightarrow \overrightarrow {IJ’} = 3\overrightarrow {IJ} \) \( \Leftrightarrow \left\{ \begin{array}{l}
x’ – 1 = 3\left( {1 + 1} \right)\\
y’ – 1 = 3\left( {1 – 2} \right)
\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}
x’ = 7\\
y’ = – 2
\end{array} \right.\) \( \Rightarrow J’\left( {7; – 2} \right).\)
Gọi \(\left( C’ \right)\) là ảnh của \(\left( C \right)\) qua phép vị tự \({{V}_{\left( I;3 \right)}}\) thì\(\left( C’ \right)\) có tâm \(J’\left( 7;-2 \right)\), bán kính \(R’=3R=6\).
Vậy \(\left( C’ \right):{{\left( x-7 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=36\).
Dạng toán 2. Tìm tâm vị tự của hai đường tròn
Phương pháp: Sử dụng phương pháp tìm tâm vị tự của hai đường tròn đã trình bày ở phần A-4.
Ví dụ 3. Cho hai đường tròn \(\left( C \right):{\left( {x – 2} \right)^2} + {\left( {y – 1} \right)^2} = 4\) và \(\left( {C’} \right):{\left( {x – 8} \right)^2} + {\left( {y – 4} \right)^2} = 16\). Tìm tâm vị tự của hai đường tròn.
Ta có: Đường tròn \(\left( C \right)\) có tâm \(I\left( {1;2} \right)\), bán kính \(R = 2\), đường tròn \(\left( {C’} \right)\) có tâm \(I’\left( {8;4} \right)\), bán kính \(R’ = 4.\)
Do \(I \ne I’\) và \(R \ne R’\) nên có hai phép vị tự \({V_{\left( {J;2} \right)}}\) và \({V_{\left( {J’; – 2} \right)}}\) biến \(\left( C \right)\) thành \(\left( {C’} \right).\)
Gọi \(J\left( {x;y} \right).\)
Với \(k = 2\), ta có: \(\overrightarrow {JI’} = 2\overrightarrow {JI} \) \( \Leftrightarrow \left\{ \begin{array}{l}
8 – x = 2\left( {2 – x} \right)\\
4 – y = 2\left( {1 – y} \right)
\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}
x = – 4\\
y = – 2
\end{array} \right.\) \( \Rightarrow J\left( { – 4; – 2} \right).\)
Tương tự với \(k = – 2\), suy ra \(J’\left( {4;2} \right).\)
[ads]
Dạng toán 3. Sử dụng phép vị tự để giải các bài toán dựng hình
Phương pháp: Để dựng một hình \(\left( H \right)\) nào đó ta quy về dựng một số điểm (đủ để xác định hình \(\left( H \right)\)) khi đó ta xem các điểm cần dựng đó là giao của hai đường trong đó một đường có sẵn và một đường là ảnh vị tự của một đường khác.
Ví dụ 4. Cho hai điểm \(B,C\) cố định và hai đường thẳng \({{d}_{1}},{{d}_{2}}\). Dựng tam giác \(ABC\) có đỉnh \(A\) thuộc \({{d}_{1}}\) và trọng tâm \(G\) thuộc \({{d}_{2}}\).
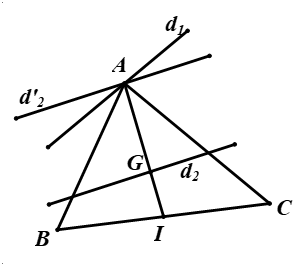
Phân tích:
Giả sử đã dựng được tam giác \(ABC\) thỏa mãn yêu cầu bài toán.
Gọi \(I\) là trung điểm của \(BC\), theo tính chất trọng tâm tam giác ta có \(\overrightarrow {IA} = 3\overrightarrow {IG} \) \( \Rightarrow {V_{\left( {I;3} \right)}}\left( G \right) = A.\)
Mà \(G \in {d_2}\) \( \Rightarrow A \in {d_2}’\), với \({d_2}’\) là ảnh của \({d_2}\) qua \({V_{\left( {I;3} \right)}}.\)
Ta lại có: \(A \in {d_1}\) \( \Rightarrow A = {d_1} \cap {d_2}’.\)
Cách dựng:
+ Dựng đường thẳng \({{d}_{2}}’\) ảnh của \({{d}_{2}}\) qua \({{V}_{\left( I;3 \right)}}\).
+ Dựng giao điểm \(A={{d}_{1}}\cap {{d}_{2}}’\).
+ Dựng giao điểm \(G=IA\cap {{d}_{2}}\).
Hai điểm \(A;G\) là hai điểm cần dựng.
Chứng minh: Rõ ràng từ cách dựng ta có \(A \in {d_1}\), \(G \in {d_2}\), \(I\) là trung điểm của \(BC\) và \({V_{\left( {I;3} \right)}}\left( G \right) = A\) \( \Rightarrow \overrightarrow {IA} = 3\overrightarrow {IG} \) \( \Rightarrow G\) là trọng tâm tam giác \(ABC.\)
Nhận xét: Số nghiệm hình của bài toán bằng số giao điểm của \({{d}_{1}}\) và \({{d}_{2}}’\).
Ví dụ 5. Cho hai đường tròn đồng tâm \(\left( {{C}_{1}} \right)\) và \(\left( {{C}_{2}} \right)\). Từ một điểm \(A\) trên đường tròn lớn \(\left( {{C}_{1}} \right)\) hãy dựng đường thẳng \(d\) cắt \(\left( {{C}_{2}} \right)\) tại \(B,C\) và cắt \(\left( {{C}_{1}} \right)\) tại \(D\) sao cho \(AB=BC=CD\).
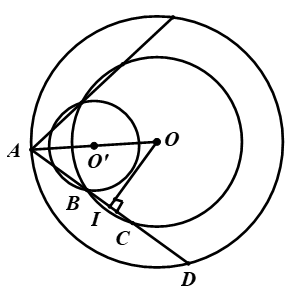
Phân tích:
Giả sử đã dựng được đường thẳng \(d\) cắt \(\left( {{C}_{1}} \right)\) tại \(D\) và \(\left( {{C}_{2}} \right)\) tại \(B,C\) sao cho \(AB=BC=CD\), khi đó \(\overrightarrow {AB} = \frac{1}{2}\overrightarrow {AC} \) \( \Rightarrow {V_{\left( {A;\frac{1}{2}} \right)}}\left( C \right) = B.\)
Mà \(C\in \left( {{C}_{2}} \right)\) nên \(B\in \left( {{C}_{2}}’ \right)\) với đường tròn \(\left( {{C}_{2}}’ \right)\) là ảnh của \(\left( {{C}_{2}} \right)\) qua \({{V}_{\left( A;\frac{1}{2} \right)}}\).
Ta lại có \(B\in \left( {{C}_{2}} \right)\) nên \(B\in \left( {{C}_{2}} \right)\cap \left( {{C}_{2}}’ \right)\).
Cách dựng:
+ Dựng đường tròn \(\left( {{C}_{2}}’ \right)\) ảnh của đường tròn \(\left( {{C}_{2}} \right)\) qua phép vị tự \({{V}_{\left( A;\frac{1}{2} \right)}}\).
+ Dựng giao điểm \(B\) của \(\left( {{C}_{2}} \right)\) và \(\left( {{C}_{2}}’ \right)\).
+ Dựng đường thẳng \(d\) đi qua \(A,B\) cắt các đường tròn \(\left( {{C}_{2}} \right),\left( {{C}_{1}} \right)\) tại \(C,D\) tương ứng.
Đường thẳng \(d\) chính là đường thẳng cần dựng.
Chứng minh:
Gọi \(I\) là trung điểm của \(AD\) thì \(I\) cũng là trung điểm của \(BC\).
Vì \({{V}_{\left( A;\frac{1}{2} \right)}}\left( C \right)=B\) nên \(AB=BC\), mặt khác \(AD\) và \(BC\) có chung trung điểm \(I\) nên \(IA = ID\), \(IB = IC\), \(ID = CD + IC\), \(IA = IB + AB\) suy ra \(CD = AB.\)
Vậy \(AB = BC = CD.\)
Nhận xét: Gọi \({{R}_{1}};{{R}_{2}}\) lần lượt là bán kính các đường tròn \(\left( {{C}_{1}} \right)\) và \(\left( {{C}_{2}} \right)\) ta có:
+ Nếu \({{R}_{1}}\ge 2{{R}_{2}}\) thì bài toán có một nghiệm hình.
+ Nếu \({{R}_{1}}<2{{R}_{2}}\) thì bài toán có hai nghiệm hình.
Dạng toán 4. Sử dụng phép vị tự để giải các bài toán tập hợp điểm
Phương pháp: Để tìm tập hợp điểm \(M\) ta có thể quy về tìm tập hợp điểm \(N\) và tìm một phép vị tự \({{V}_{\left( I;k \right)}}\) nào đó sao cho \({{V}_{\left( I;k \right)}}\left( N \right)=M\) suy ra quỹ tích điểm \(M\) là ảnh của quỹ tích \(N\) qua \({{V}_{\left( I;k \right)}}\).
Ví dụ 6. Cho đường tròn \(\left( O;R \right)\) và một điểm \(I\) nằm ngoài đường tròn sao cho \(OI=3R\), \(A\) là một điểm thay đổi trên đường tròn \(\left( O;R \right)\). Phân giác trong góc \(\widehat{IOA}\) cắt \(IA\) tại điểm \(M\). Tìm tập hợp điểm \(M\) khi \(A\) di động trên \(\left( O;R \right)\).
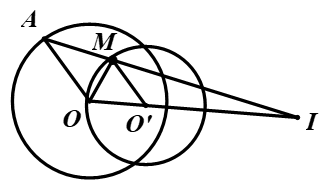
Theo tính chất đường phân giác ta có \(\frac{{MI}}{{MA}} = \frac{{OI}}{{OA}} = \frac{{3R}}{R} = 3\) \( \Rightarrow IM = \frac{3}{4}IA\) \( \Rightarrow \overrightarrow {IM} = \frac{3}{4}\overrightarrow {IA} .\)
Suy ra \({{V}_{\left( I;\frac{3}{4} \right)}}\left( A \right)=M\), mà \(A\) thuộc đường tròn \(\left( O;R \right)\) nên \(M\) thuộc \(\left( O’;\frac{3}{4}R \right)\) ảnh của \(\left( O;R \right)\) qua \({{V}_{\left( I;\frac{3}{4} \right)}}\).
Vậy tập hợp điểm \(M\) là \(\left( O’;\frac{3}{4}R \right)\) ảnh của \(\left( O;R \right)\) qua \({{V}_{\left( I;\frac{3}{4} \right)}}\).
Ví dụ 7. Cho tam giác \(ABC\). Qua điểm \(M\) trên cạnh \(AB\) vẽ các đường song song với các đường trung tuyến \(AE\) và \(BF\), tương ứng cắt \(BC\) và \(CA\) tai \(P,Q\) . Tìm tập hợp điểm \(R\) sao cho \(MPRQ\) là hình bình hành.
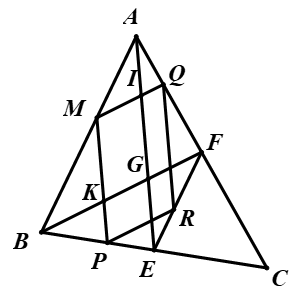
Gọi \(I = MQ \cap AE\), \(K = MP \cap BF\) và \(G\) là trọng tâm của tam giác \(ABC.\)
Ta có: \(\frac{{MI}}{{BG}} = \frac{{AM}}{{AB}} = \frac{{AQ}}{{AF}} = \frac{{IQ}}{{GF}}\) \( \Rightarrow \frac{{MI}}{{IQ}} = \frac{{BG}}{{GF}} = 2\) \( \Rightarrow \overrightarrow {MI} = \frac{2}{3}\overrightarrow {MQ} .\)
Tương tự ta có \(\overrightarrow {MK} = \frac{2}{3}\overrightarrow {MP} .\)
Từ đó ta có \(\overrightarrow {MG} = \overrightarrow {MI} + \overrightarrow {MK} \) \( = \frac{2}{3}\overrightarrow {MQ} + \frac{2}{3}\overrightarrow {MP} \) \( = \frac{2}{3}\overrightarrow {MR} .\)
Do đó \(\overrightarrow {GR} = – \frac{1}{2}\overrightarrow {GM} \) \( \Rightarrow {V_{\left( {G; – \frac{1}{2}} \right)}}\left( M \right) = R.\)
Mà \(M\) thuộc cạnh \(AB\) nên \(R\) thuộc ảnh của cạnh \(AB\) qua \({{V}_{\left( G;-\frac{1}{2} \right)}}\) đoạn chính là đoạn \(EF\).
Vậy tập hợp điểm \(R\) là đoạn \(EF\).
Dạng toán 5. Sử dụng phép vị tự để chứng minh các tính chất hình học phẳng
Ví dụ 8. Trên cạnh \(AB\) của tam giác \(ABC\) lấy các điểm \(M,N\) sao cho \(AM=MN=NB\), các điểm \(E,F\) lần lượt là trung điểm của các cạnh \(CB,CA\), gọi \(P\) là giao điểm của \(BF\) và \(CN\), \(Q\) là giao điểm của \(AE\) với \(CM\). Chứng minh \(PQ//AB\).
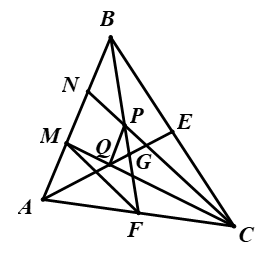
Gọi \(G\) là trọng tâm của tam giác \(ABC\).
Ta có \(MF\) là đường trung bình của tam giác \(ACN\) nên \(MF\parallel CN\), mặt khác \(N\) là trung điểm của \(MB\) nên \(P\) là trung điểm của \(BF\).
Ta có: \(\overrightarrow {GP} = \overrightarrow {BP} – \overrightarrow {BG} \) \( = \frac{1}{2}\overrightarrow {BF} – \frac{2}{3}\overrightarrow {BF} \) \( = – \frac{1}{6}\overrightarrow {BF} = \frac{1}{4}\overrightarrow {GB} .\)
Tương tự \(\overrightarrow {GQ} = \frac{1}{4}\overrightarrow {GA} .\)
Vậy \({{V}_{\left( G;\frac{1}{4} \right)}}\left( B \right)=P\) và \({{V}_{\left( G;\frac{1}{4} \right)}}\left( A \right)=Q\) suy ra \(PQ//AB\).
Ví dụ 9. Cho tam giác \(ABC\). Gọi \(I,J,M\) lần lượt là trung điểm của \(AB,AC,IJ\). Đường tròn \(\left( O \right)\) ngoại tiếp tam giác \(AIJ\) cắt \(AO\) tại \(D\). Gọi \(E\) là hình chiếu vuông góc của \(D\) trên \(BC\). Chứng minh \(A,M,E\) thẳng hàng.
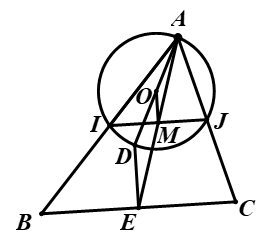
Xét phép vị tự \({V_{\left( {A;2} \right)}}\), ta có: \(\overrightarrow {AB} = 2\overrightarrow {AI} \), \(\overrightarrow {AC} = 2\overrightarrow {AJ} \) nên \({V_{\left( {A;2} \right)}}\left( I \right) = B\), \({V_{\left( {A;2} \right)}}\left( J \right) = C\), do đó \({V_{\left( {A;2} \right)}}\) biến tam giác \(AIJ\) thành tam giác \(ABC\), suy ra phép vị tự này biến đường tròn \(\left( O \right)\) thành đường tròn \(\left( O’ \right)\) ngoại tiếp tam giác \(ABC\).
Do \(\overrightarrow {AD} = 2\overrightarrow {AO} \) \( \Rightarrow {V_{\left( {A;2} \right)}}\left( O \right) = D\) \( \Rightarrow O’ \equiv D\) hay \(D\) là tâm của đường tròn ngoại tiếp tam giác \(ABC.\)
Giả sử \({V_{\left( {A;2} \right)}}\left( M \right) = M’\) khi đó \(OM \bot IJ\) \( \Rightarrow DM’ \bot BC\) \( \Rightarrow M’ \equiv E.\)
Vậy \({{V}_{\left( A;2 \right)}}\left( M \right)=E\) nên \(A,M,E\) thẳng hàng.