Bài viết hướng dẫn phương pháp giải bài toán tìm tọa độ giao điểm, đếm số giao điểm của các đồ thị hàm số trong chương trình Giải tích 12.
I. PHƯƠNG PHÁP GIẢI TOÁN
Cho hai hàm số $y = f(x)$ có đồ thị $\left( {{C_1}} \right)$ và $y = g(x)$ có đồ thị là $\left( {{C_2}} \right).$ Khi đó số giao điểm của hai đồ thị $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$ chính bằng số nghiệm phân biệt của phương trình: $f(x) = g(x).$
Chú ý: Trục hoành có phương trình $y = 0$, nên phương trình hoành độ giao điểm của đồ thị hàm số $y = f(x)$ với trục hoành là: $f(x) = 0.$
Trong nội dung chuyên đề này, ta xét hai nội dung cụ thể:
+ Cho hàm số, tìm số giao điểm của các đồ thị.
+ Cho bảng biến thiên hoặc đồ thị hàm số, tìm số giao điểm của các đồ thị.
II. VÍ DỤ MINH HỌA
Ví dụ 1. Cho hàm số $f(x) = {x^3} – 6{x^2} + 11x – 6.$ Tìm số giao điểm của đồ thị hàm số đã cho với trục hoành.
Phương trình hoành độ giao điểm đồ thị hàm số với trục hoành là:
${x^3} – 6{x^2} + 11x – 6 = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 1}\\
{x = 2}\\
{x = 3}
\end{array}} \right..$
Do đó đồ thị hàm số đã cho cắt trục hoành tại $3$ điểm phân biệt.
Ví dụ 2. Cho hàm số $f(x) = \frac{{{x^2} – 2x – 3}}{{{x^2} – x + 1}}.$ Tìm tọa độ giao điểm của đồ thị hàm số đã cho với trục hoành.
Phương trình hoành độ giao điểm đồ thị hàm số với trục hoành là:
$\frac{{{x^2} – 2x – 3}}{{{x^2} – x + 1}} = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 1}\\
{x = 3}
\end{array}} \right..$
Do đó đồ thị hàm số đã cho cắt trục hoành tại $2$ điểm $A(-1;0)$ và $B(3;0).$
Ví dụ 3. Cho hàm số $f(x) = {x^3} + 4x – 2$, $g(x) = 3{x^2} + 4x – 4.$ Tìm số giao điểm của hai đồ thị hàm số đã cho.
Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là:
${x^3} + 4x – 2 = 3{x^2} + 4x – 4$ $ \Leftrightarrow {x^3} – 3{x^2} + 2 = 0.$
$ \Leftrightarrow (x – 1)\left( {{x^2} – 2x – 2} \right) = 0.$
$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 1}\\
{x = 1 \pm \sqrt 3 }
\end{array}} \right..$
Do đó hai đồ thị hàm số đã cho cắt nhau tại $3$ điểm phân biệt.
Ví dụ 4. Cho hàm số $f(x) = \frac{{3x + 1}}{{x + 1}}$, $g(x) = 3 – x.$ Tìm tọa độ giao điểm của hai đồ thị hàm số đã cho.
Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là:
$\frac{{3x + 1}}{{x + 1}} = 3 – x$ $ \Rightarrow {x^2} + x – 2 = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 1}\\
{x = – 2}
\end{array}} \right.$ (kiểm tra lại thỏa mãn $x \ne – 1$).
Do đó hai đồ thị hàm số đã cho cắt nhau tại $2$ điểm là: $A(1;2)$ và $B(-2;5).$
Ví dụ 5. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ bên. Tìm số nghiệm của phương trình: $3f(x) – 2 = 0.$

Ta có $3f(x) – 2 = 0$ $ \Leftrightarrow f(x) = \frac{2}{3}.$
Từ đồ thị hàm số đã cho, vẽ đường thẳng $y = \frac{2}{3}.$

Khi đó số giao điểm của đường thẳng $y = \frac{2}{3}$ với đồ thị hàm số $y = f(x)$ chính là số nghiệm phân biệt của phương trình $3f(x) – 2 = 0.$
Quan sát hình vẽ, ta thấy phương trình $3f(x) – 2 = 0$ có ba nghiệm phân biệt.
Ví dụ 6. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới đây.

Tìm số nghiệm của phương trình: $3f(x) + 17 = 0.$
Ta có $3f(x) + 17 = 0$ $ \Leftrightarrow f(x) = – \frac{{17}}{3}.$
Khi đó số giao điểm của đường thẳng $y = \frac{{ – 17}}{3}$ với đồ thị hàm số $y = f(x)$ chính là số nghiệm phân biệt của phương trình $3f(x) + 17 = 0.$
Ta có $ – 6 < \frac{{ – 17}}{3} < – 5.$ Quan sát hình vẽ, ta thấy đường thẳng $y = \frac{{ – 17}}{3}$ cắt đồ thị hàm số $y = f(x)$ tại $4$ điểm phân biệt nên phương trình $3f(x) + 17 = 0$ có bốn nghiệm phân biệt.
III. BÀI TẬP TRẮC NGHIỆM
Bài 1. Cho hàm số $f(x) = {x^3} + 3{x^2} – 3x – 5.$ Xác định số giao điểm của đồ thị hàm số đã cho với trục hoành.
A. $1.$
B. $2.$
C. $3.$
D. $0.$
Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là:
${x^3} + 3{x^2} – 3x – 5 = 0$ $ \Leftrightarrow (x + 1)\left( {{x^2} + 2x – 5} \right) = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 1}\\
{x = – 1 \pm \sqrt 6 }
\end{array}} \right..$
Do đó số giao điểm của đồ thị hàm số đã cho với trục hoành là $3.$
Chọn đáp án C.
Bài 2. Cho hàm số $f(x) = {x^4} – 4{x^2} + 3.$ Xác định số giao điểm của đồ thị hàm số đã cho với trục hoành.
A. $1.$
B. $2.$
C. $3.$
D. $4.$
Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là:
${x^4} – 4{x^2} + 3 = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{x^2} = 1}\\
{{x^2} = 3}
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \pm 1}\\
{x = \pm \sqrt 3 }
\end{array}} \right..$
Do đó số giao điểm của đồ thị hàm số đã cho với trục hoành là $4.$
Chọn đáp án D.
Bài 3. Cho hàm số $f(x) = {x^3} – 3x + 5$ $\left( {{C_1}} \right)$ và $g(x) = – {x^2} – 3x + 7$ $\left( {{C_2}} \right).$ Xác định số giao điểm của hai đồ thị hàm số đã cho.
A. $3.$
B. $1.$
C. $2.$
D. $4.$
Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là:
${x^3} – 3x + 5 = – {x^2} – 3x + 7$ $ \Leftrightarrow {x^3} + {x^2} – 2 = 0$ $ \Leftrightarrow x = 1.$
Do đó số giao điểm của hai đồ thị hàm số đã cho là $1.$
Chọn đáp án B.
Bài 4. Cho hàm số $f(x) = \frac{{3x – 2}}{{x – 1}}$ $\left( {{C_1}} \right)$ và $g(x) = x + 2$ $\left( {{C_2}} \right).$ Xác định tọa độ giao điểm của hai đồ thị hàm số đã cho.
A. $A(0;2)$, $B(2;4).$
B. $A(2;2)$, $B(0;4).$
C. $A(2;0)$, $B(4;0).$
D. $A(0;2)$, $B(4;2).$
Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là:
$\frac{{3x – 2}}{{x – 1}} = x + 2$ (điều kiện $x \ne 1$) $ \Leftrightarrow 3x – 2 = {x^2} + x – 2$ $ \Leftrightarrow {x^2} – 2x = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0}\\
{x = 2}
\end{array}} \right..$
Do đó tọa độ giao điểm của hai đồ thị hàm số là: $A(0;2)$, $B(2;4).$
Chọn đáp án A.
Bài 5. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ bên. Xác định số nghiệm của phương trình $6f(x) + 15 = 0.$

A. $1.$
B. $3.$
C. $2.$
D. $0.$
Ta có $6f(x) + 15 = 0$ $ \Leftrightarrow f(x) = – \frac{5}{2}.$
Vẽ đường thẳng $y = – \frac{5}{2}$ trên cùng hệ trục tọa độ với đồ thị hàm số $y = f(x).$

Quan sát hình vẽ ta thấy đường thẳng $y = – \frac{5}{2}$ cắt đồ thị hàm số $y = f(x)$ tại $3$ điểm phân biệt nên phương trình $6f(x) + 15 = 0$ có $3$ nghiệm phân biệt.
Chọn đáp án B.
Bài 6. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ dưới đây. Xác định số nghiệm của phương trình $4f(x) – 3 = 0.$

A. $6.$
B. $3.$
C. $5.$
D. $4.$
Ta có $4f(x) – 3 = 0$ $ \Leftrightarrow f(x) = \frac{3}{4}.$
Vẽ đường thẳng $y = \frac{3}{4}$ trên cùng hệ trục tọa độ với đồ thị hàm số $y = f(x).$

Quan sát hình vẽ ta thấy đường thẳng $y = \frac{3}{4}$ cắt đồ thị hàm số $y = f(x)$ tại $6$ điểm phân biệt nên phương trình $4f(x) – 3 = 0$ có $6$ nghiệm phân biệt.
Chọn đáp án A.
Bài 7. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ dưới đây. Xác định số nghiệm của phương trình $f(x) – x = 4.$

A. $1.$
B. $3.$
C. $2.$
D. $4.$
Ta có $f(x) – x = 4$ $ \Leftrightarrow f(x) = x + 4.$
Vẽ đường thẳng $y = x + 4$ trên cùng hệ trục tọa độ với đồ thị hàm số $y = f(x).$

Quan sát hình vẽ ta thấy đường thẳng $y = x + 4$ cắt đồ thị hàm số $y = f(x)$ tại $3$ điểm phân biệt nên phương trình $f(x) – x = 4$ có $3$ nghiệm phân biệt.
Chọn đáp án B.
Bài 8. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ dưới đây. Xác định số nghiệm của phương trình $2f(x) – 3 = 0.$

A. $1.$
B. $0.$
C. $2.$
D. $3.$
Ta có $2f(x) – 3 = 0$ $ \Leftrightarrow f(x) = \frac{3}{2}.$
Vẽ đường thẳng $y = \frac{3}{2}$ trên cùng hệ trục tọa độ với đồ thị hàm số $y = f(x).$

Quan sát hình vẽ ta thấy đường thẳng $y = \frac{3}{2}$ cắt đồ thị hàm số $y = f(x)$ tại $2$ điểm phân biệt nên phương trình $2f(x) – 3 = 0$ có $2$ nghiệm phân biệt.
Chọn đáp án C.
Bài 9. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới đây. Xác định số nghiệm của phương trình $f(x) + 1 = 0.$

A. $3.$
B. $2.$
C. $4.$
D. $1.$
Ta có $f(x) + 1 = 0$ $ \Leftrightarrow f(x) = – 1.$
Quan sát bảng biến thiên, ta thấy đường thẳng $y = -1$ cắt đồ thị hàm số $y = f(x)$ tại một điểm.
Nếu không chú ý $\mathop {\lim }\limits_{x \to + \infty } y = – 1$ thì nhiều bạn sẽ chọn đáp án là đường thẳng đường thẳng $y = -1$ cắt đồ thị hàm số $y = f(x)$ tại hai điểm phân biệt. Điều này không đúng.
Chọn đáp án D.
Bài 10. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới đây. Xác định số nghiệm của phương trình ${f^2}(x) – 3f(x) + 2 = 0.$

A. $3.$
B. $5.$
C. $4.$
D. $6.$
Ta có ${f^2}(x) – 3f(x) + 2 = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{f(x) = 1}\\
{f(x) = 2}
\end{array}} \right..$
Nhận xét: $ – 4 < 1 < 2.$
Quan sát bảng biến thiên, ta thấy đường thẳng $y=1$ cắt đồ thị hàm số $y = f(x)$ tại $3$ điểm phân biệt, đường thẳng $y=2$ cắt đồ thị hàm số $y=f(x)$ tại $2$ điểm phân biệt. Do đó số nghiệm của phương trình đã cho là $5$ nghiệm.
Chú ý: Tại $x = -1$, đạo hàm $y’$ không xác định nhưng hàm số $y$ vẫn xác định do đó khi xét $f(x) = 2$ thì vẫn nhận nghiệm $x = -1.$ Khi chúng ta đọc bảng biến thiên của hàm số nên để ý điểm đặc biệt này.
Chọn đáp án B.
IV. BÀI TẬP TỰ LUYỆN
Bài 1. Cho hàm số $y = {x^3} – 4{x^2} + 3.$ Xác định số giao điểm của đồ thị của hàm số đã cho với trục hoành.
A. $3.$
B. $2.$
C. $1.$
D. $0.$
Bài 2. Cho hàm số $y = – {x^3} + {x^2} + x – 1.$ Xác định số giao điểm của đồ thị của hàm số đã cho với trục hoành.
A. $3.$
B. $2.$
C. $1.$
D. $0.$
Bài 3. Cho hàm số $y = {x^4} – 3{x^3} + 2x.$ Xác định số giao điểm của đồ thị của hàm số đã cho với trục hoành.
A. $4.$
B. $2.$
C. $1.$
D. $3.$
Bài 4. Cho hàm số $y = {x^4} + 2x – 3.$ Xác định số giao điểm của đồ thị của hàm số đã cho với trục hoành.
A. $4.$
B. $3.$
C. $0.$
D. $2.$
Bài 5. Cho hàm số $y = x – 2 – \frac{6}{{x – 1}}.$ Xác định số giao điểm của đồ thị của hàm số đã cho với trục hoành.
A. $4.$
B. $3.$
C. $1.$
D. $2.$
Bài 6. Cho hàm số $f(x) = {x^3} + 3x – 2$ và $g(x) = 3{x^2} – 1.$ Xác định tọa độ giao điểm của hai đồ thị hàm số đã cho.
A. $A(1;0).$
B. $A(1;2).$
C. $A(-1;2).$
D. $A(-1;2).$
Bài 7. Cho hàm số $f(x) = {x^4} + 2{x^2} + 5$ và $g(x) = {x^2} + 7.$ Xác định tọa độ giao điểm của hai đồ thị hàm số đã cho.
A. $A(1;8)$, $B(-1;8).$
B. $A(-1;6)$, $B(-1;6).$
C. $A(-1;–8)$, $B(1;-8).$
D. $A(8;1)$, $B(-8;1).$
Bài 8. Cho hàm số $f(x) = \frac{{3x + 1}}{{x + 1}}$ và $g(x) = 2x + 1.$ Xác định tọa độ giao điểm của hai đồ thị hàm số đã cho.
A. $A(0;1).$
B. $A(–1;0).$
C. $A(0;-1).$
D. $A(0;4).$
Bài 9. Cho hàm số $f(x) = \frac{{x + 3}}{{x – 1}}$ và $g(x) = 2x + 1.$ Biết đồ thị của hai hàm số đã cho cắt nhau tại hai điểm phân biệt $A\left( {{x_1};{y_1}} \right)$, $B\left( {{x_2};{y_2}} \right)$ sao cho ${x_1} < {x_2}.$ Tính giá trị biểu thức $P = 3{x_1} + {x_2}.$
A. $P=3.$
B. $P=2.$
C. $P=-1.$
D. $P=5.$
Bài 10. Cho hàm số $f(x) = \frac{{ – x + 2}}{{x + 1}}$ và $g(x) = 3x + 2.$ Biết đồ thị của hai hàm số đã cho cắt nhau tại hai điểm phân biệt $A\left( {{x_1};{y_1}} \right)$, $B\left( {{x_2};{y_2}} \right)$ sao cho ${x_1} < {x_2}.$ Tính giá trị biểu thức $P = {x_1} + 2{y_1} + 3{x_2} + 4{y_2}.$
A. $P=-18.$
B. $P=-2.$
C. $P=-1.$
D. $P=3.$
Bài 11. Cho hàm số $y = f(x)$ là có đồ thị như hình vẽ bên. Xác định số nghiệm của phương trình $3f(x) + 7 = 0.$

A. $1.$
B. $0.$
C. $2.$
D. $3.$
Bài 12. Cho hàm số $y = f(x)$ là có đồ thị như hình vẽ bên. Xác định số nghiệm của phương trình $3f(x) – 11 = 0.$

A. $1.$
B. $3.$
C. $2.$
D. $4.$
Bài 13. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ bên. Xác định số nghiệm của phương trình $2f(x) + 7 = 0.$

A. $1.$
B. $3.$
C. $2.$
D. $4.$
Bài 14. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ bên. Xác định số nghiệm phân biệt của phương trình $3f(x) + x + 11 = 0.$

A. $1.$
B. $2.$
C. $3.$
D. $4.$
Bài 15. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ bên. Xác định số nghiệm phân biệt của phương trình $2f(x) – x = 2.$

A. $3.$
B. $2.$
C. $1.$
D. $4.$
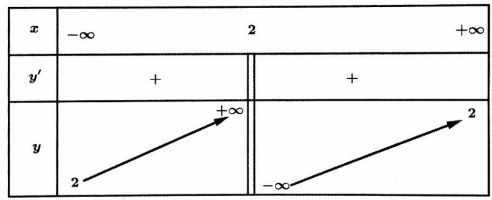
Bài 16. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới đây. Xác định số nghiệm phân biệt của phương trình $2f(x) – 3 = 0.$
A. $3.$
B. $2.$
C. $1.$
D. $0.$
Bài 17. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới đây. Xác định số nghiệm phân biệt của phương trình ${f^2}(x) – 3f(x) + 2 = 0.$

A. $3.$
B. $1.$
C. $2.$
D. $0.$
Bài 18. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới đây. Xác định số nghiệm phân biệt của phương trình ${f^2}(x) + 5f(x) + 4 = 0.$

A. $3.$
B. $4.$
C. $6.$
D. $5.$
Bài 19. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới đây. Xác định số nghiệm phân biệt của phương trình ${f^2}(x) – 7f(x) + 12 = 0.$

Bài 20. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới đây. Xác định số nghiệm phân biệt của phương trình ${f^2}(x) + 7f(x) + 6 = 0.$

A. $5.$
B. $4.$
C. $6.$
D. $7.$
V. BẢNG ĐÁP ÁN BÀI TẬP TỰ LUYỆN
1. A.
2. B.
3. A.
4. D.
5. D.
6. B.
7. A.
8. A.
9. C.
10. B.
11. A.
12. D.
13. D.
14. C.
15. A.
16. C.
17. A.
18. D.
19. A.
20. B.
Nguồn: toanmath.com
